Continuity equation

Coming from four-current.

If we reduce one more dimension to simplify we we can get a deeper understanding. Imagine particles moving in a 1-dimensional world, for which we draw a spacetime diagram like this one:

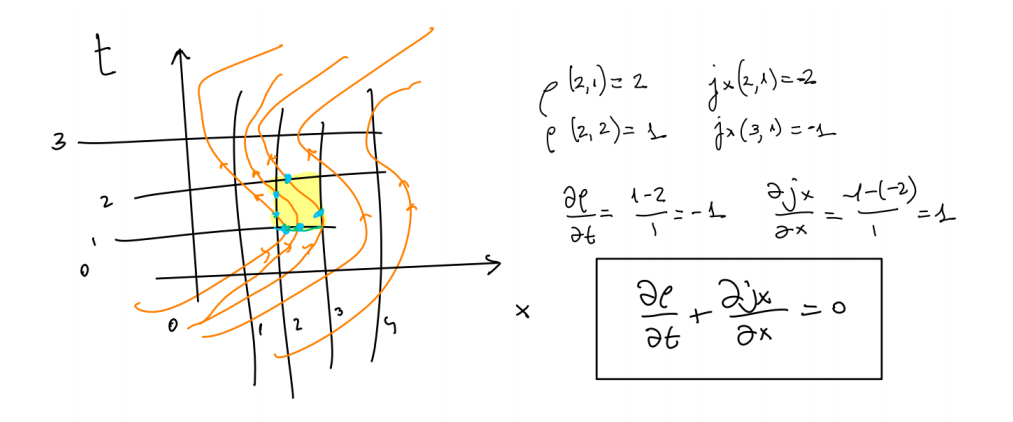
In a little piece of this space (from $x=2$ to $x=3$, for example), we pass from having 2 particles to having 1 particle at times $t=1$ and $t=2$ respectively. This corresponds to the fact that 2 particles have left the room (to the left) and one has arrived (from the right).

I imagine $\rho(x,t)$ and $j_x(x,t)$ like infinitesimal "flow meter devices" that I install on spacetime event $(x,t)$ to measure how many particles go throw it. Observe that we have a tacit sign convention for $j_x$ depending on the sense you go through the vertical line. At a first glance, this convention is not needed for $\rho$ since time always flows forward. But we can assume a negative density like something travelling backward in time (like Feynman said for positrons).

If we consider that this flow is a vector field with components $J=(j_x,j_y,j_z,\rho)$ in Minkowski space $\mathbb{M}^4$, then continuity equation is nothing but the statement

where $\mbox{div}$ stands for divergence

More elaborated:

Example 4.22 in @olver86.

Perhaps the most graphic physical illustration of the relationship between conserved densities and fluxes comes from the equations of compressible, in-viscid fluid motion. Let $x \in \mathbb{R}^n$ represent the spatial coordinates, and $u = u(x, t) \in \mathbb{R}^n$ the velocity of a fluid particle at position $x$ and time $t$. Further let $\rho(x, t)$ be the density, and $p(x, t)$ the pressure; in the particular case of isentropic (constant entropy) flow, pressure $p = P(\rho)$ will depend on density alone. The equation of continuity takes the form

where $\text{Div}(\rho u) = \sum_{j=1}^{n} \frac{\partial (\rho u_j)}{\partial x_j}$ is the spatial divergence. This equation is already in the form of a conservation law, with density $T = \rho$ and flux $X = \rho u$. This leads to the integral equation for the conservation of mass

Here $\int_V \rho dx$ is clearly the mass of fluid within the domain $V$, while $\rho u \cdot n$, with $n$ the unit normal to $\partial V$, is the instantaneous mass flux of fluid out of a point on the boundary $\partial V$. Thus we see that the net change in mass inside $V$ equals the flux of fluid into $V$. In particular, if the normal component of velocity $u \cdot n$ on $\partial V$ vanishes, there is no net change in mass within the domain $V$, and we have a law of conservation of mass:

$$\int_V \rho dx = \text{constant}.$$

________________________________________

________________________________________

________________________________________

Author of the notes: Antonio J. Pan-Collantes

antonio.pan@uca.es